Gradient descent is an optimization algorithm that tries to find the minimum of a function by following its gradient.
The gradient
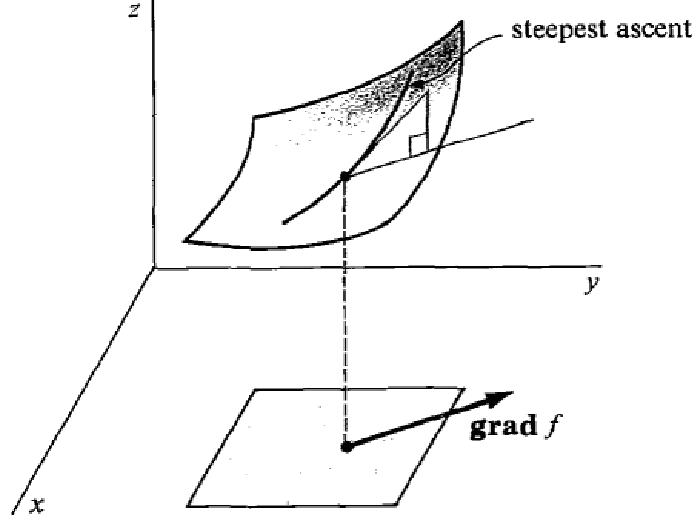
The gradient of a differentiable function is a vector that points in the direction of greatest rate of increase of .
Mathematically, it is defined by the partial derivatives:
Gradient descent
Since the gradient is directed along the steepest ascent, it’s opposite is directed along the steepest descent. The gradient descent algorithm aims at finding a function’s minimum by taking successive steps directed along :
where is the size of the step at iteration .
def gradient_descent(f, x_0, max_steps, step_size):
x = x_0
for step in range(max_steps):
x = x - step_size * gradient(of=f, at=x)
return x
Pitfalls
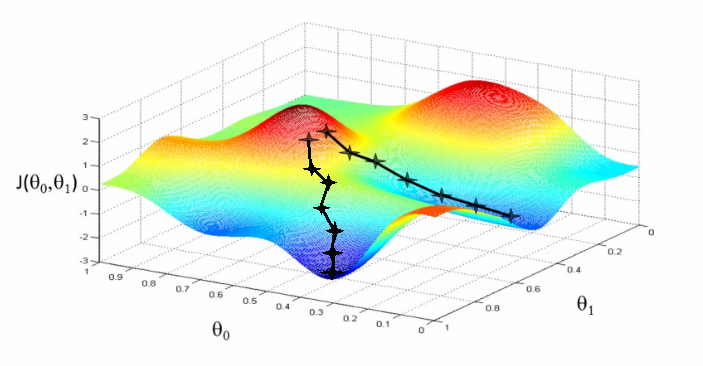
As illustrated on the picture above, the gradient descent algorithm might get stuck in a local minimum. Since it always follows the steepest descent, there is no way to get away from a local minimum once it has been reached.
Illustration
The contour plot below displays the contours line of a function (think of it as seeing the surface from above). Click anywhere on it to start a gradient descent.