Derivative, Gradient and Jacobian unified

A summary about scalar and vector derivatives.

Functions of scalars

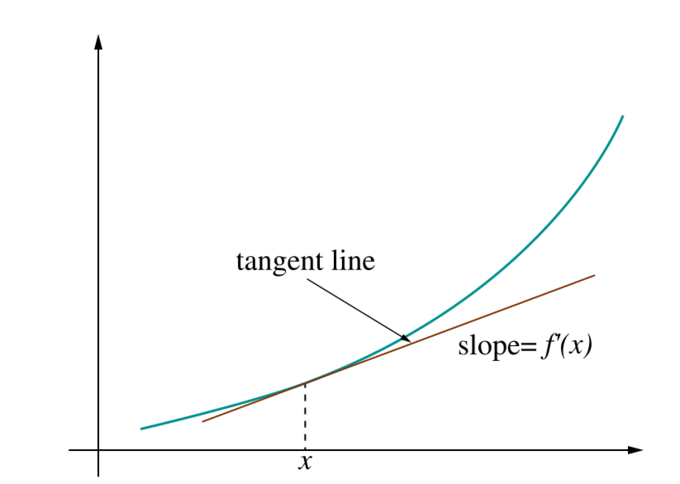
Let $f: \realset \to \realset$ a function. For $x \in \realset$, the derivative of $f$ at point $x$ is:

$$\frac{\partial}{\partial x} f(x) = \lim_{h \to 0} \frac{f(x + h) - f(h)}{h} \quad \in \realset$$

This number is the slope of the tangent to the curve described by $f$.

Vector functions of scalars

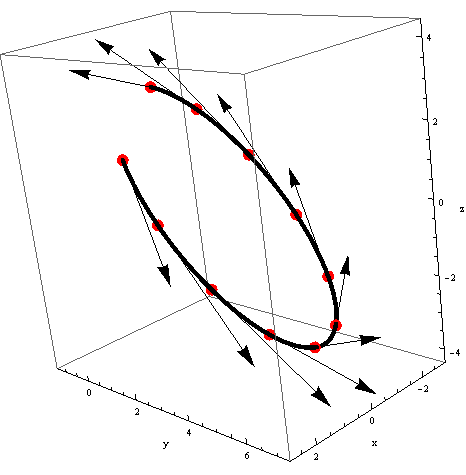
Let $\vec{f}: \realset \to \realvset{M}$ a function. For $x \in \realset$, the derivative of $\vec{f}$ at point $x$ is:

$$\frac{\partial}{\partial x} \vec{f}(x) = \lim_{h \to 0} \frac{\vec{f}(x + h) - \vec{f}(x)}{h}$$

Which is the vector of the partial derivative:

$$\frac{\partial}{\partial x} \vec{f}(x) = \begin{pmatrix} \frac{\partial}{\partial x}f_1(x) \\ \vdots \\ \frac{\partial}{\partial x}f_M(x)\end{pmatrix} \quad \in \realvset{M}$$

This vector is tangent to the parametric curve described by $f$.

Functions of vectors

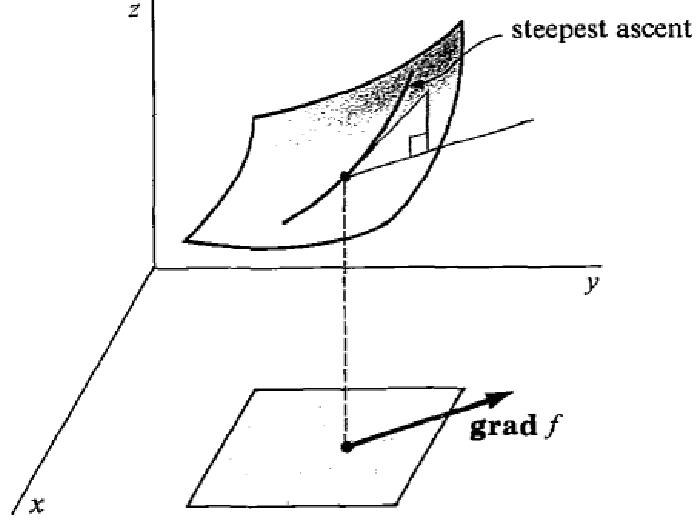
Let $f: \realvset{N} \to \realset$ a function. For $\vec{x} \in \realvset{N}$, the derivative of $f$ at point $\vec{x}$ is:

$$\frac{\partial}{\partial \vec{x}} f(\vec{x}) = (\frac{\partial}{\partial x_1} f(\vec{x}), \cdots, \frac{\partial}{\partial x_N} f(\vec{x})) \quad \in \realvset{1 \times N}$$

We call this row vector the gradient of $\vec{f}$. It is noted:

$$\grad f(\vec{x}) = \frac{\partial}{\partial \vec{x}} f(\vec{x})$$

This vector is tangent to the suface described by $f$ and directed along the steepest ascent of $f$.

Vector functions of vectors

Let $\vec{f}: \realvset{N} \to \realvset{M}$ a function. For $\vec{x} \in \realvset{M}$, the derivative of $\vec{f}$ at point $\vec{x}$ can be writen in two equivalent forms.

Since $\frac{\partial}{\partial \vec{x}} f_1(\vec{x})$ is the derivative of a scalar function with respect to a vector, we have:

$$\frac{\partial}{\partial \vec{x}} \vec{f}(\vec{x}) = \begin{pmatrix} \leftarrow & \frac{\partial}{\partial \vec{x}}f_1(\vec{x}) & \rightarrow \\ & \vdots & \\ \leftarrow & \frac{\partial}{\partial \vec{x}}f_M(\vec{x}) & \rightarrow \\ \end{pmatrix}$$

Which corresponds to the following matrix in $\realvset{N \times M}$:

$$\frac{\partial}{\partial \vec{x}} \vec{f}(\vec{x}) = \begin{pmatrix} \frac{\partial}{\partial x_1}f_1(\vec{x}) & \cdots & \frac{\partial}{\partial x_N}f_1(\vec{x}) \\ & \vdots & \\ \frac{\partial}{\partial x_1}f_M(\vec{x}) & \cdots & \frac{\partial}{\partial x_N}f_M(\vec{x}) \\ \end{pmatrix}$$

This matrix is called the jacobian of $\vec{f}$.

Actually, when all the components of $\vec{x}$ are fixed except $x_1$, $\vec{f}(\vec{x})$ can be considered as a function of the scalar $x_1$. In this view, $\frac{\partial}{\partial x_1} \vec{f}(\vec{x})$ is the derivative of a vector function with respect to the scalar $x_1$, and we have:

$$\frac{\partial}{\partial \vec{x}} \vec{f}(\vec{x}) = \begin{pmatrix} \uparrow & & \uparrow \\ \frac{\partial}{\partial x_1} \vec{f}(\vec{x}),& \cdots,& \frac{\partial}{\partial x_N} \vec{f}(\vec{x}) \\ \downarrow & & \downarrow \end{pmatrix}$$