Why do we care about convexity?

In machine learning, the best parameters for a model are chosen so as to minimize the training objective. Strictly convex functions are paticularly interesting because they have a unique global minimum.

Furthermore, for strict and non-sctrict convex functions, every local minimum is a global minimum.

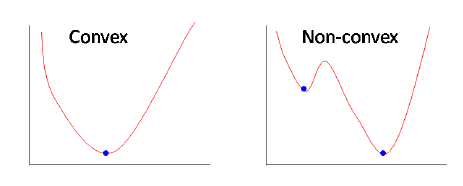
Visually, a convex function “curves up”, without any bends the other way.

What is convexity?

A function is convex if and only if a segment joining two points on its curve always stays above the curve. $\forall 0 \leq t \leq 1$:

$$f(t \vec{a} + (1-t) \vec{b}) \leq t f(\vec{a}) + (1-t) f(\vec{b})$$

The function is strictly convex when the inequality is strict.

Caracterization of convex functions

1. Sum of convex functions are also convex.
2. A differentiable function of one variable is convex on an interval iff it lies above all of its tangents: $f(x) \geq f(y) + f'(y)(x-y)$.
3. A differentiable function of several variables is convex on a compact iff it lies above its linearization: $f(v) \geq f(\linparamv) + \nabla f(\linparamv)^{\top}(v-\linparamv)$
4. A twice differentiable function of one variable is convex on an interval iff its second derivative is non-negative.