What is a residual?

The residual $\ve$ is the error vector between the true output vector $\vy$ and its estimate $\hat{\vy}$:

$$\ve = \vy - \hat{\vy}$$

Residuals for linear regressions

When $\hat{\vy}$ is produced by a linear model, the residual represent the aspects of $\vy$ that cannot be explained by the columns of the design matrix $\mx$ :

$$\ve = \vy - \mx\hat{\vw}$$

Since $\hat{vy} = \mx\hat{\vw}$ is a vector in the linear space spanned by the columns of $\mx$, the residual is a vector outside of this linear space, pointing towards $\vy$.

Note: and when the MSE-loss is used, the residual is orthogonal to this linear space.

Let $\mathcal{M}(\mx)$ be the column space of $\mx$. The vector $\hat{\vy}$ is in this linear subspace while $\vy$ isn’t. This is illustrated on the picture below.

.

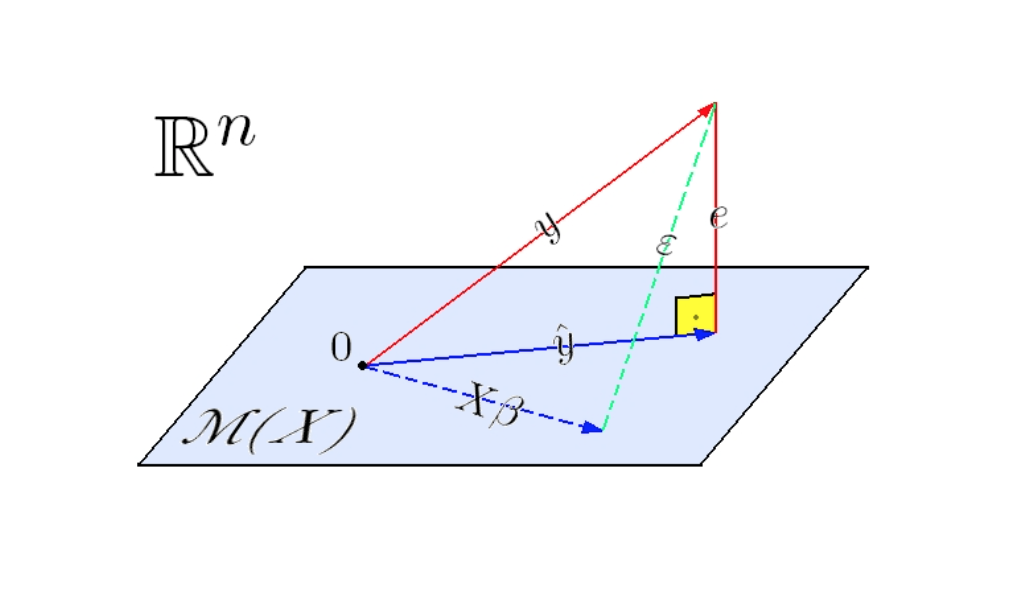Residuals for OLS

The parameter vector $\hat{\vw}$ can be expressed using a closed-form formula in the case of an OLS regression;

$$\hat{vw} = (\mx^{\top}\mx)^{-1}\mx^{\top}\vy$$

Pluging this formula into the definition of a residual, we get:

$$\ve = \vy - \underbrace{\mx(\mx^{\top}\mx)^{-1}\mx^{\top}}_{\mh}\vy$$

$\mh$ is the hat-matrix (because it puts a hat on $\vy$). Rewriting the equality with $\vy$ as factor, we get:

$$\ve = (\mi_\sn - \mh)\vy$$

As mentioned above, for OLS regressions, the residual is a vector orthogonal to the column space of $\mx$.