The change of basis matrix

$\def\sa{a} \def\sb{b} \def\sc{c} \def\sd{d} \def\se{e} \def\sf{f} \def\sg{g} \def\sh{h} \def\si{i} \def\sj{j} \def\sk{k} \def\sl{l} \def\sm{m} \def\sn{n} \def\so{o} \def\sp{p} \def\sq{q} \def\sr{r} \def\ss{s} \def\st{t} \def\su{u} \def\sv{v} \def\sw{w} \def\sx{x} \def\sy{y} \def\sz{z} \def\va{\vec{a}} \def\vb{\vec{b}} \def\vc{\vec{c}} \def\vd{\vec{d}} \def\ve{\vec{e}} \def\vf{\vec{f}} \def\vg{\vec{g}} \def\vh{\vec{h}} \def\vi{\vec{i}} \def\vj{\vec{j}} \def\vk{\vec{k}} \def\vl{\vec{l}} \def\vm{\vec{m}} \def\vn{\vec{n}} \def\vo{\vec{o}} \def\vp{\vec{p}} \def\vq{\vec{q}} \def\vr{\vec{r}} \def\vs{\vec{s}} \def\vt{\vec{t}} \def\vu{\vec{u}} \def\vv{\vec{v}} \def\vw{\vec{w}} \def\vx{\vec{x}} \def\vy{\vec{y}} \def\vz{\vec{z}} \def\ga{\mathfrak{A}} \def\gb{\mathfrak{B}} \def\gc{\mathfrak{C}} \def\gd{\mathfrak{D}} \def\ge{\mathfrak{E}} \def\gf{\mathfrak{F}} \def\gg{\mathfrak{G}} \def\gh{\mathfrak{H}} \def\gi{\mathfrak{I}} \def\gj{\mathfrak{J}} \def\gk{\mathfrak{K}} \def\gl{\mathfrak{L}} \def\gm{\mathfrak{M}} \def\gn{\mathfrak{N}} \def\go{\mathfrak{O}} \def\gp{\mathfrak{P}} \def\gq{\mathfrak{Q}} \def\gr{\mathfrak{R}} \def\gs{\mathfrak{S}} \def\gt{\mathfrak{T}} \def\gu{\mathfrak{U}} \def\gv{\mathfrak{V}} \def\gw{\mathfrak{W}} \def\gx{\mathfrak{X}} \def\gy{\mathfrak{Y}} \def\gz{\mathfrak{Z}} \def\ra{A} \def\rb{B} \def\rc{C} \def\rd{D} \def\re{E} \def\rf{F} \def\rg{G} \def\rh{H} \def\ri{I} \def\rj{J} \def\rk{K} \def\rl{L} \def\rm{M} \def\rn{N} \def\ro{O} \def\rp{P} \def\rq{Q} \def\rr{R} \def\rs{S} \def\rt{T} \def\ru{U} \def\rv{V} \def\rw{W} \def\rx{X} \def\ry{Y} \def\rz{Z} \def\rva{\vec{A}} \def\rvb{\vec{B}} \def\rvc{\vec{C}} \def\rvd{\vec{D}} \def\rve{\vec{E}} \def\rvf{\vec{F}} \def\rvg{\vec{G}} \def\rvh{\vec{H}} \def\rvi{\vec{I}} \def\rvj{\vec{J}} \def\rvk{\vec{K}} \def\rvl{\vec{L}} \def\rvm{\vec{M}} \def\rvn{\vec{N}} \def\rvo{\vec{O}} \def\rvp{\vec{P}} \def\rvq{\vec{Q}} \def\rvr{\vec{R}} \def\rvs{\vec{S}} \def\rvt{\vec{T}} \def\rvu{\vec{U}} \def\rvv{\vec{V}} \def\rvw{\vec{W}} \def\rvx{\vec{X}} \def\rvy{\vec{Y}} \def\rvz{\vec{Z}} \def\seta{A} \def\setb{B} \def\setc{C} \def\setd{D} \def\sete{E} \def\setf{F} \def\setg{G} \def\seth{H} \def\seti{I} \def\setj{J} \def\setk{K} \def\setl{L} \def\setm{M} \def\setn{N} \def\seto{O} \def\setp{P} \def\setq{Q} \def\setr{R} \def\sets{S} \def\sett{T} \def\setu{U} \def\setv{V} \def\setw{W} \def\setx{X} \def\sety{Y} \def\setz{Z} \def\fa{a} \def\fb{b} \def\fc{c} \def\fd{d} \def\fe{e} \def\ff{f} \def\fg{g} \def\fh{h} \def\fi{i} \def\fj{j} \def\fk{k} \def\fl{l} \def\fm{m} \def\fn{n} \def\fo{o} \def\fp{p} \def\fq{q} \def\fr{r} \def\fs{s} \def\ft{t} \def\fu{u} \def\fv{v} \def\fw{w} \def\fx{x} \def\fy{y} \def\fz{z} \def\fA{A} \def\fB{B} \def\fC{C} \def\fD{D} \def\fE{E} \def\fF{F} \def\fG{G} \def\fH{H} \def\fI{I} \def\fJ{J} \def\fK{K} \def\fL{L} \def\fM{M} \def\fN{N} \def\fO{O} \def\fP{P} \def\fQ{Q} \def\fR{R} \def\fS{S} \def\fT{T} \def\fU{U} \def\fV{V} \def\fW{W} \def\fX{X} \def\fY{Y} \def\fZ{Z} \def\ma{A} \def\mb{B} \def\mc{C} \def\md{D} \def\me{E} \def\mf{F} \def\mg{G} \def\mh{H} \def\mi{I} \def\mj{J} \def\mk{K} \def\ml{L} \def\mm{M} \def\mn{N} \def\mo{O} \def\mp{P} \def\mq{Q} \def\mr{R} \def\ms{S} \def\mt{T} \def\matu{U} \def\mv{V} \def\mw{W} \def\mx{X} \def\my{Y} \def\mz{Z} \def\loss{\mathcal{L}} \newcommand{\dkl}[2]{D_{\text{KL}}\mathopen{}\paren{#1\,||\,#2}} \newcommand{\dataset}{S} \newcommand{\ndataset}{N} \newcommand{\idataset}{n} \newcommand{\inputRV}{\mathcal{X}} \newcommand{\inputvec}{\vec{x}} \newcommand{\ninputvec}[1]{\vec{x}_{#1}} \newcommand{\iinputvec}[1]{x_{#1}} \newcommand{\niinputvec}[2]{x_{#1, #2}} \newcommand{\icpnt}{i} \newcommand{\inputmatrix}{X} \newcommand{\inputdim}{D} \newcommand{\outputval}{y} \newcommand{\ioutputval}[1]{y_{#1}} \newcommand{\outputvec}{\vec{y}} \newcommand{\trainset}{S_{\text{train}}} \newcommand{\testset}{S_{\text{test}}} \newcommand{\truemodel}{f_{\text{true}}} \newcommand{\trainedmodel}{f_{\trainset}} \newcommand{\linmodel}[1]{f_{#1}} \newcommand{\bestmodel}{f^{*}} \newcommand{\model}{f} \newcommand{\hyperparam}{\lambda} \newcommand{\linparamv}{\vec{w}} \newcommand{\ilinparam}[1]{w_{#1}} \newcommand{\indivloss}{l} \newcommand{\modelclass}{\mathcal{F}} \newcommand{\linclass}{\modelclass_{\text{lin}}} \newcommand{\g}{\mathcal{G}} \newcommand{\gmse}{\g_{\text{MSE}}} \newcommand{\glasso}{\g_{\text{lasso}}} \newcommand{\gridge}{\g_{\text{ridge}}} \newcommand{\glogit}{\g_{\logit}} \newcommand{\l}{\mathcal{L}} \newcommand{\lmse}{\l_{\text{MSE}}} \newcommand{\lmae}{\l_{\text{MAE}}} \newcommand{\llasso}{\l_{\text{lasso}}} \newcommand{\lridge}{\l_{\text{ridge}}} \newcommand{\llogit}{\l_{\logit}} \newcommand{\logit}{\sigma} \newcommand{\reg}{\mathcal{R}} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\mean}{mean} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator*{\span}{span} \DeclareMathOperator*{\var}{var} \DeclareMathOperator*{\bias}{bias} \newcommand{\expectation}{\mathbb{E}} \newcommand{\brak}[1]{\left[#1\right]} \newcommand{\paren}[1]{\left(#1\right)} \newcommand{\realset}{\mathbb{R}} \newcommand{\realvset}[1]{\realset^{#1}} \newcommand{\prob}{\mathbb{P}} \newcommand{\gaussian}{\mathcal{N}} \newcommand{\iid}{\stackrel{\text{i.i.d.}}{\sim}} \newcommand{\abs}[1]{\left\lvert#1\right\rvert} \newcommand{\norm}[1]{\left\lVert#1\right\rVert} \newcommand{\normtwo}[1]{\norm{#1}_{2}} \newcommand{\normone}[1]{\norm{#1}_{1}} \newcommand{\card}[1]{\left\lvert#1\right\rvert} \newcommand{\grad}{\nabla} \newcommand{\dconv}{\stackrel{d}{\to}} \newcommand{\pconv}{\stackrel{p}{\to}} \newcommand{\rva}[1]{#1} \newcommand{\rve}[1]{\vec{#1}} \newcommand{\obs}[1]{#1} \newcommand{\vobs}[1]{\vec{#1}} \newcommand{\distrib}[1]{#1} \newcommand{\distribof}[2]{#1_{#2}} \newcommand{\density}[1]{#1} \newcommand{\densityof}[2]{#1_{#2}} \newcommand{\distributed}{\sim} \newcommand{\const}[1]{#1} \newcommand{\fun}[1]{#1}$

This article explains the intuition behind the change of basis matrix.

Change of basis

You can represent a vector $\color{blue}{\vec{v}}$ by its coordinates in a basis. For instance, here are the coordinates for the vector $\vec{v}$ in two different basis $(e) = (e_1, e_2)$ and $(f) = (f_1, f_2)$ :

Base 1 ( $e_1$ , $e_2$ )

Base1 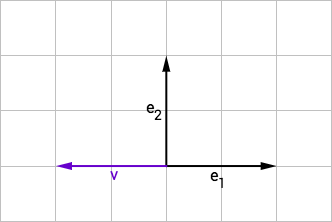\[\color{blue}{\vec{v}} = \begin{pmatrix}-1\\0\end{pmatrix}^e = -1 e_1 + 0 e_2 \]

Base 2 ( $f_1$ , $f_2$ )

Base2 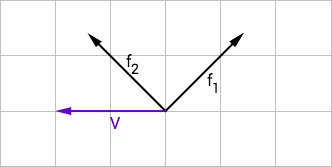\[\color{blue}{\vec{v}} = \begin{pmatrix}-0.5\\+0.5\end{pmatrix}^f = -0.5 f_1 + 0.5 f_2 \]

The change of basis matrix

We can use a matrix to transform the coordinates of $\vec{v}$ in the basis $(e)$ into the coordinates in the basis $(f)$ . This matrix is called the change of basis matrix.

How do we find this matrix? Since it takes the coordinates of a vector in basis $(e)$ and gives the coordinates in the basis $(f)$ , we can start by expressing the vectors $e_1$ and $e_2$ in basis $(f)$ .

In basis $(e)$ : $e_1 = \begin{pmatrix}1\\0\end{pmatrix}^e$ and $e_2 = \begin{pmatrix}0\\1\end{pmatrix}^e$

…and…

In basis $(f)$ : $\color{red}{e_1} = \begin{pmatrix}\color{red}{0.5}\\\color{red}{-0.5}\end{pmatrix}^f$ and $\color{green}{e_2} = \begin{pmatrix}\color{green}{0.5}\\\color{green}{0.5}\end{pmatrix}^f$ .

So we are looking for the matrix $M_{f\leftarrow e}$ such that:

$\begin{pmatrix}\color{red}{0.5}\\\color{red}{-0.5}\end{pmatrix}^f = M_{f\leftarrow e} \cdot \begin{pmatrix}1\\0\end{pmatrix}^e$

…and…

$\begin{pmatrix}\color{green}{0.5}\\\color{green}{0.5}\end{pmatrix}^f = M_{f\leftarrow e} \cdot \begin{pmatrix}0\\1\end{pmatrix}^e$

Since $M_{f\leftarrow e} \cdot (1, 0)^\top$ is the first column of $M_{f\leftarrow e}$ and $M_{f\leftarrow e} \cdot (0, 1)^\top$ is the second column of $M_{f\leftarrow e}$ , we find that the change of basis matrix is the matrix made of the vector column of the old basis $(e)$ expressed in the new basis $(f)$ . We note $\vec{v}^f$ the coordinates of vector $\vec{v}$ in base $(f)$ .

$M_{f\leftarrow e} = \begin{bmatrix}\color{red}{\vec{e_1}}^f & \color{green}{\vec{e_2}}^f\end{bmatrix} = \begin{pmatrix} \color{red}{0.5} & \color{green}{0.5} \\ \color{red}{-0.5} & \color{green}{0.5} \end{pmatrix}$

Using this matrix, we can translate the coordinates for $\color{blue}{\vec{v}}$ from basis $(e)$ to basis $(f)$ :

$\color{blue}{\vec{v}} : \begin{pmatrix}-0.5\\+0.5\end{pmatrix}^f = M_{f \leftarrow e} \cdot \begin{pmatrix}-1\\0\end{pmatrix}^e$

From vector notation to sum notation

Sometimes, it’s useful to remember that matrix multiplication can be expressed as a sum of vectors using linearity.

The change of basis matrix allows us to write equations where some vectors are expressed in base $(f)$ (left hand side) while others are in base $(e)$ (right hand side).

Using the notation $\vec{v}^f$ for the coordinates of vector $\vec{v}$ in base $(f)$ :

$\begin{pmatrix}\color{purple}{a}\\\color{orange}{b}\end{pmatrix}^f = M_{f \leftarrow e} \cdot \begin{pmatrix}\color{chocolate}{c}\\\color{gray}{d}\end{pmatrix}^e$ $\color{purple}{a} \, \vec{f_1}^f + \color{orange}{b} \, \vec{f_2}^f = M_{f \leftarrow e} \cdot ( \color{chocolate}{c} \, \vec{e_1}^e + \color{gray}{d} \, \vec{e_2}^e )$ $\color{purple}{a} \, \vec{f_1}^f + \color{orange}{b} \, \vec{f_2}^f = \color{chocolate}{c} \, (M_{f \leftarrow e} \cdot \vec{e_1}^e) + \color{gray}{d} \, (M_{f \leftarrow e} \cdot \vec{e_2}^e)$ $\color{purple}{a} \, \vec{f_1}^f + \color{orange}{b} \, \vec{f_2}^f = \color{chocolate}{c} \, \vec{e_1}^f + \color{gray}{d} \, \vec{e_2}^f$

Where every vector in the last equation is expressed in base $(f)$ .

The change of basis matrix

Change of basis

Base 1 (e_1, e_2)

Base 2 (f_1, f_2)

The change of basis matrix

From vector notation to sum notation

Base 1 ( $e_1$ , $e_2$ )

Base 2 ( $f_1$ , $f_2$ )